Calculation Example – Simple harmonic vibration part 2
Contents [show]
A single point with mass m is vibrating harmonically. The displacement x from point of balance is governed by the differential equation
where ω is a positive constant.
b) What is the speed, the acceleration, and the force at the mass as a function of time t and constants A, B.
Solution
The derivative of x(t)=A sinωt+B cos ωt
is the speed u(t)=x'(t)=Aω cosωt-B ωsinωt
And the derivative of speed is the acceleration
a(t)=u'(t)=x''(t)=-〖ω^2 Α sin〗ωt-ω^2 B cosωt
The force at the mass is
Selected Topics
Want to read more like this?

Calculation Example – Simple harmonic vibration part1
Oct, 04, 2017 | EducationA single point with mass m is vibrating harmonically. The displacement x from point of balance is go...

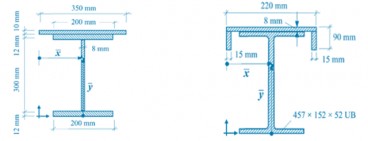
Calculation of the cross-sectional area and the position of centroid
Apr, 04, 2024 | EducationThe problem: Determine the cross-sectional area and the position of the centroid for the sectio...
Calculation of the second moments of area
Apr, 12, 2024 | EducationThe problem: Determine the second moments of area, Ixx and Iyy, for the sections indicated in...

Calculation Example - Calculate the equation of the elastic curve.
Jan, 25, 2017 | EducationCalculate the equation of the elastic curve .Determine the pinned beam’s maximum deflection. EI cons...

Calculation Example - Calculate the location of support.
Mar, 01, 2017 | EducationCalculate the distance x for locating roller support so that the moment on the beam at point B is ze...

Calculation Example – Beam with inner hinge (Part B). Calculate the member diagrams.
Mar, 17, 2016 | EducationCalculate the member diagrams. Solution We have already calculated the external beam rea...
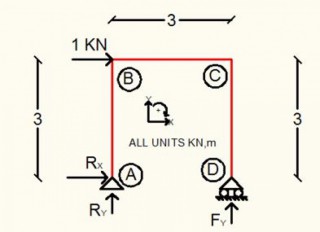
Calculation Example – Frame analysis.
Apr, 13, 2016 | EducationCalculate the reactions and member forces. Solution We calculate the reactions. Section 1 0...
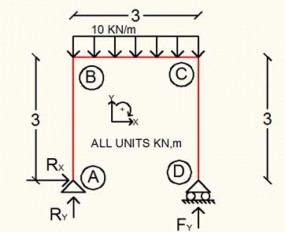
Calculation Example – Frame analysis – Uniform Load
May, 09, 2016 | EducationCalculate the reactions and member forces. Solution We calculate the reactions. ...

Beams: maximum moment
Jun, 07, 2022 | EducationFind the maximum moment of the above beam which is subjected to triangular vertical load. SOLUTION:...
Trending

Diaphragms
Structural stability
Nominal flexural strength of a reinforced concrete beam

Calculate the Maximum Shear Stress
Truss deflection using the unit load method

Overhanging beam: shear force and bending moment calculation

Calculation Example – Beam with inner hinge (Part A). Find the Reactions

