Calculation of the cross-sectional area and the position of centroid

The problem:

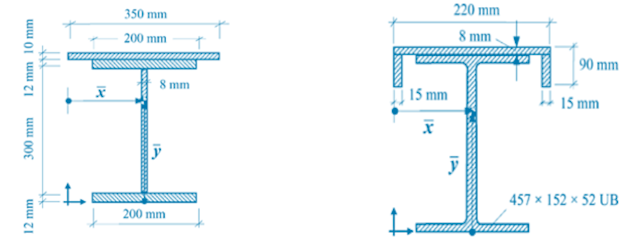
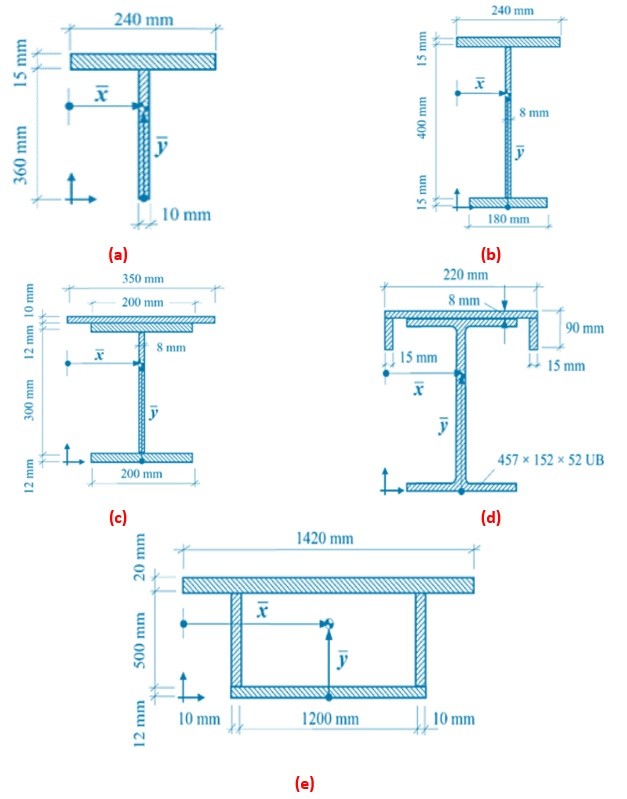
Determine the cross-sectional area and the position of the centroid for the sections shown in Figures 1a to 1e. Please consider that the origin of the coordinate system is located at the lower left corner of every section (see each Figure below).

Tip: It is given that the total height and the area of the 457 x 152 x 52 UB section are: h = 449.8mm and A = 66.6cm², respectively.

The solution:

a)       i) cross-sectional area

A = 240 x 15 + 360 x 10 = 7200mm²

ii) position of centroid

x̄ = 240/2 =120mm

ȳ = [(240 x 15) x 367.5 + (360 x 10) x 180] / 7200 = 273.75mm

b)      i) cross-sectional area

A = 240 x 15 + 400 x 8 + 180 x 15 = 9500mm²

ii) position of centroid

x̄ = 240/2 =120mm

ȳ = [(240 x 15) x 422.5 + (400 x 8) x 215 +(180 x 15) x 7.5] / 9500 = 234.66mm

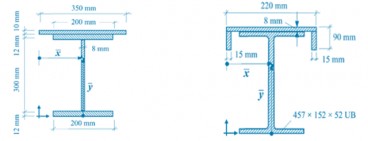
c)       i) cross-sectional area

A = 350 x 10 + 200 x 12 + 300 x 8 + 200 x 12 = 10700mm²

ii) position of centroid

x̄ = 350/2 =175mm

ȳ = [(350 x 10) x 329 + (200 x 12) x 318 + (300 x 8) x 162 + (200 x 12) x 6] / 10700 = 216.63mm

d)      i) cross-sectional area

A = 220 x 8 + 82 x 15 + 82 x 15 + 6660 = 10880mm²

ii) position of centroid

x̄ = 220/2 =110mm

ȳ ₌ [(220 x 8) x (449.8 + 4) + (82 x 15) x (449.8-41) + (82 x 15) x (449.8-41) + 6660 x 449.8/2] / 10880 = 303.51mm

e)      i) cross-sectional area

A = 1420 x 20 + 500 x 10 + 500 x 10 + 1220 x 12 = 53040mm²

ii) position of centroid

x̄ = 1420/2 =710mm

ȳ = [(1420 x 20) x 522+ (500 x 10) x 262 + (500 x 10) x 262 + (1220 x 12) x 6] / 53040 = 330.56mm