Truss deflection using the unit load method

Contents [hide show]

Description
Selected Topics

Given:

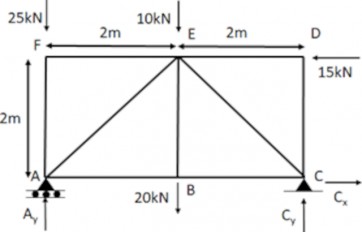
A pin-jointed truss is given in Figure 1. Determine the vertical displacement of joint E using the unit load method. All the members have cross-sectional area of 250mm and same modulus of elasticity 200GPa.

Figure 1: The pin-jointed plane truss considered.

Solution:

According to the unit load method, which is also known as virtual work method, the deflection of a joint of truss is given by the formula: δ_Ε = (ΣNnL)/AE.

The member forces should be calculated two times. First we will calculate member forces "N" due to the real loading and then "n" due to unit virtual load applied at the point of required deflection (in this case joint E). Tensile forces are considered as positive and compressive forces as negative. L is the length of the member, A is area of cross-section of the member and E is modulus of elasticity of the material.

Step 1: The member forces "N" due to real load are calculated as follows:

(i) ΣF_x = 0 -> C_x - 15 = 0 -> C_x =15kN

(ii) ΣF_y = 0 -> A_y + C_y - 25 -10 - 20 = 0 -> A_y + C_y = 55

(iii) ΣM_z = 0 ->; A_y x 0 + C_y x 4 – C_x x 0 - 20 x 2 + 15 x 2 - 10 x 2 + 25 x 0 =0 -> C_y = 7.5kN

Therefore, A_y = 47.5kN.

It is outlined that it has been considered that z-axis is perpendicular to the plane and passes through joint A.

Step 2: Calculation of member forces "n" due to unit virtual load applied at E as shown in Figure 2. As the unit load is applied at center of the truss, the support reactions at A and C will be both 0.5kN. Considering the equilibrium of joint D, we get F_DE =0 and F_DC =0. Similarly, the equilibrium conditions at joint F gives F_FE =0 and F_FA =0. Consider the equilibrium of joint B along y-axis we get F_BE =0. Considering the equilibrium of joint A gives the following.