Beams: maximum moment
Contents [show]
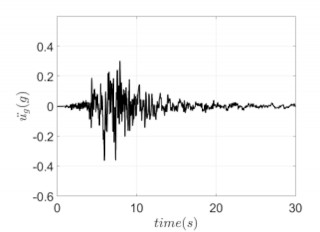
Find the maximum moment of the above beam which is subjected to triangular vertical load.
SOLUTION:
ΣΜΒ = 0 → ΑΥ –(1/2)ql(l/3)=0 → ΑΥ = (1/6)ql
ΣFY = 0 → ql/6 + BΥ –(1/2)ql=0 → BΥ = (1/3)ql
Assuming the equilibrium in distance x from the A end:
ΣΜX = 0 → (1/6)qlx – (1/2)(x/l)qx(x/3) - Mx = 0 → Mx = (ql/6)x(1 - x2/l2)
ΣFY = 0 → (1/6)ql –(1/2)(x/l)qx - Qx=0 → Qx =(ql/6)(1 - 3x2/l2)
Maximum M means zero Q:
QX = 0 → (ql/6)(1 - 3x2/l2) = 0 → x = l/ √ 3
maxM = (ql/6)(l/ √ 3 )(1 - l2/(3l2)) → maxM = (ql2/ 9√ 3 )
Selected Topics
Want to read more like this?

Calculate the location of point load
Feb, 14, 2019 | EducationCalculate the distance x for locating point load so that the moment on the beam at point B is zero....
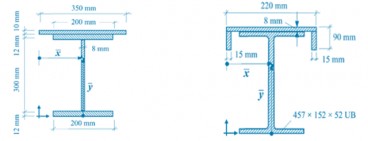
Calculation of the second moments of area
Apr, 12, 2024 | EducationThe problem: Determine the second moments of area, Ixx and Iyy, for the sections indicated in...
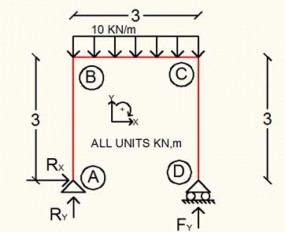
Calculation Example – Frame analysis – Uniform Load
May, 09, 2016 | EducationCalculate the reactions and member forces. Solution We calculate the reactions. ...
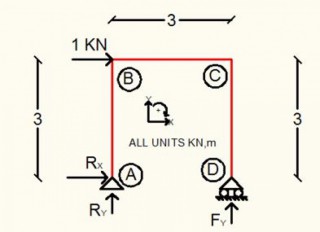
Calculation Example – Frame analysis.
Apr, 13, 2016 | EducationCalculate the reactions and member forces. Solution We calculate the reactions. Section 1 0...

Calculation of the cross-sectional area and the position of centroid
Apr, 04, 2024 | EducationThe problem: Determine the cross-sectional area and the position of the centroid for the sectio...
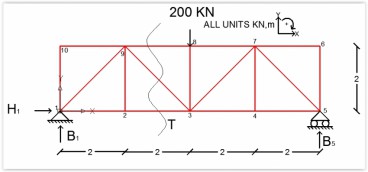
Calculate the Axial Forces of the Truss Members
May, 16, 2019 | EducationFind the axial forces of the members 2-3, 9-3 of the truss for the given loads. Solution...

Shear bolt connection EC3
Mar, 18, 2019 | EducationCheck the shear connection for the IPE450-S275 for the design shear VEd=500KN. Bolts M20-8.8, plate...
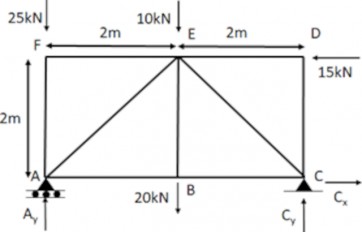
Truss deflection using the unit load method
Aug, 28, 2023 | EducationGiven: A pin-jointed truss is given in Figure 1. Determine the vertical displacement of join...

Method of sections
Sep, 07, 2023 | EducationPlease determine the forces in the members BC, GC and GF of the pin-jointed plane truss shown in F...
Trending

Diaphragms
Structural stability
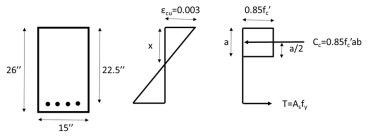
Nominal flexural strength of a reinforced concrete beam

Calculate the Maximum Shear Stress

Overhanging beam: shear force and bending moment calculation

Calculation Example – Beam with inner hinge (Part A). Find the Reactions

Calculation Example – Plastic Neutral Axis.