Calculation of the second moments of area

Contents [show]
The problem:
Determine the second moments of area, Ixx and Iyy, for the sections indicated in Figures 2a to 2e.
Tip: It is given that the total height and the area of the 457 x 152 x 52 UB section are: h = 449.8mm and A = 66.6cm2, respectively. Furthermore, the second moments of area are Ixx = 21400cm4 and Iyy = 645cm4.

The solution:
a) i) y1 and y2

y1 = 360 + 7.5 – 273.75 = 93.75mm
y2 = 273.75 – 180 = 93.75mm
ii) Ixx
Ixx = (240 x 153)/12 + 240 x 15 x 93.752 + (10 x 3603)/12 + 360 x 10 x 93.752 = 102.23 x 106 mm4
iii) Iyy
Iyy = (15 x 2403)/12 + (360 x 103)/12 = 17.31 x 106 mm4
b) i) y1, y2 and y3

y1 = 15 + 400 + 7.5 – 234.66 = 187.84mm
y2 = 234.66 – (15+200) = 19.66mm
y3 = 234.66 – 7.5 = 227.16mm
ii) Ixx
Ixx = (240 x 153)/12 + 240 x 15 x 187.842 + (8 x 4003)/12 + 400 x 8 x 19.662 + (180 x 153)/12 + 180 x 15 x 227.162 = 310.37 x 106 mm4
iii) Iyy
Iyy = (15 x 2403)/12 + (400 x 83)/12 + (15 x 1803)/12 = 24.59 x 106 mm4
c) i) y1, y2, y3 and y4

y1 = 15 + 300 + 12 + 5 - 216.63 = 112.37mm
y2 = 12 + 300 + 6 - 216.63 = 101.37mm
y3 = 216.63 – (12+150) = 54.63mm
y4 = 216.63 – 6 = 210.63mm
ii) Ixx
Ixx = (350 x 103)/12 + 350 x 10 x 112.372 + (200 x 123)/12 + 200 x 12 x 101.372 + (8 x 3003)/12 + 8 x 300 x 54.632 + (200 x 123)/12 + 200 x 12 x 210.632= 200.58 x 106 mm4
iii) Iyy
Iyy = (10 x 3503)/12 + 2 x (12 x 2003)/12 + (300 x 83)/12 = 51.74 x 106 mm4
d) i) x1, x2, y1, y2 and y3

x1 = 110 – 7.5 = 102.50mm
x2 = 110 – 7.5 = 102.50mm
y1 = 449.8 + 4 -303.51 = 150.29mm
y2 = 449.8 - 41 -303.51 = 105.29mm
y3 = 303.51 – (449.8/2) = 78.61mm
ii) Ixx
Ixx = (220 x 83)/12 + 220 x 8 x 150.292 + 2 x (15 x 823)/12 + 15 x 82 x 105.292 + (21400 x104) + 6660 x 78.612= 323.57 x 106 mm4
iii) Iyy
Iyy = (8 x 2203)/12 + 2 x [(82 x 153)/12 + (82 x 15 x 102.52)] + 645 x 104 = 39.44 x 106 mm4
e) i) x1, x2, y1, y2 and y3

x1 = 1200/2 + 5 = 605mm
x2 = 1200/2 + 5 = 605mm
y1 = 12 + 500 + 10 – 330.56 = 191.44mm
y2 = 330.56 – (12 +250) = 68.56mm
y3 = 330.56 – 6 = 324.56mm
ii) Ixx
Ixx = (1420 x203)/12 + 1420 x 20 x 191.442 + 2 x (10 x 5003)/12 + 10 x 500 x 68.562 + (1220 x123)/12 + 1220 x 12 x 324.562= 2839.47 x 106 mm4
iii) Iyy
Iyy = (20 x 14203)/12 + 2 x [(500 x 103)/12 + (10 x 500 x 6052)] + (12 x 12203)/12 = 10248.30 x 106 mm4
Selected Topics
Want to read more like this?

Calculation of the cross-sectional area and the position of centroid
Apr, 04, 2024 | EducationThe problem: Determine the cross-sectional area and the position of the centroid for the sectio...
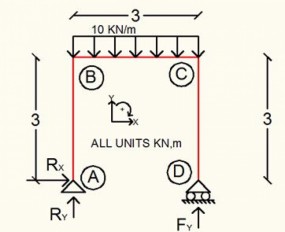
Calculation Example – Frame analysis – Uniform Load
May, 09, 2016 | EducationCalculate the reactions and member forces. Solution We calculate the reactions. ...
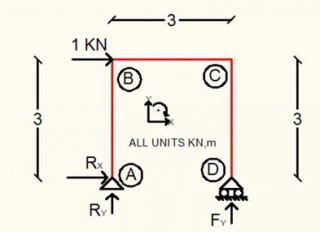
Calculation Example – Frame analysis.
Apr, 13, 2016 | EducationCalculate the reactions and member forces. Solution We calculate the reactions. Section 1 0...

Beams: maximum moment
Jun, 07, 2022 | EducationFind the maximum moment of the above beam which is subjected to triangular vertical load. SOLUTION:...

Calculation Example - Calculate the equation of the elastic curve.
Jan, 25, 2017 | EducationCalculate the equation of the elastic curve .Determine the pinned beam’s maximum deflection. EI cons...

Calculation Example – Beam with inner hinge (Part B). Calculate the member diagrams.
Mar, 17, 2016 | EducationCalculate the member diagrams. Solution We have already calculated the external beam rea...

Calculate the location of point load
Feb, 14, 2019 | EducationCalculate the distance x for locating point load so that the moment on the beam at point B is zero....

Method of sections
Sep, 07, 2023 | EducationPlease determine the forces in the members BC, GC and GF of the pin-jointed plane truss shown in F...

Allowable shear force of the girder
Jan, 15, 2020 | EducationCalculate the maximum allowable shear force Vmax for the girder. The welded steel girder is having...
Trending

Diaphragms
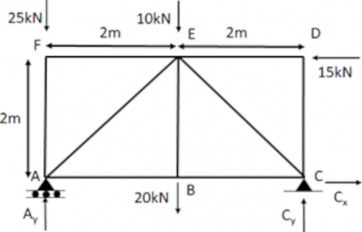
Truss deflection using the unit load method
Structural stability
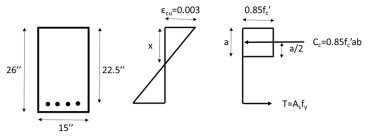
Nominal flexural strength of a reinforced concrete beam

Overhanging beam: shear force and bending moment calculation

Calculate the Maximum Shear Stress

Calculation Example – Plastic Neutral Axis.