Bentley's Bentley Webinar: Mastering RAM Concept for Preliminary Design: Extracting Key Information for Accurate Estimates begins at 16 Oct 2024
Bentley's Bentley Webinar: Mastering RAM Concept for Preliminary Design: Extracting Key Information for Accurate Estimates begins at 16 Oct 2024
Create a free account and view content that fits your specific interests in structural engineering Learn More
Contents [show]
A single point with mass m is vibrating harmonically. The displacement x from point of balance is governed by the differential equation
where ω is a positive constant.
a) Show that
and
are equivalent.
Solution
So the form is x(t)=A sinωt+B cosωt
where
x(t)=A sinωt+B cosωt
with
Selected Topics
Calculation Example: Natural Periods of Vibration for SystemsCalculation Example: Axial Force On A ColumnCalculation Example: Shear force On A ColumnCalculation Example: Overturning Moment for Shear panelCalculation Example: Calculate the Change in Length of a Rod loaded in extensionCalculation Example - Calculate the Axial Forces on the Truss MembersCalculation Example - Calculate the member diagramsCalculation Example - Calculate the member diagrams for the beamCalculation Example – Beam with inner hinge (Part A). Find the ReactionsCalculation Example – Beam with inner hinge (Part B). Calculate the member diagrams.Calculation Example – Frame analysis.Calculation Example – Frame analysis – Uniform LoadCalculation Example – Find the Center of Gravity (Surface)Calculation Example – Design bolted connection of tension plates (EC3)Calculation Example – Cantilever BeamCalculation Example – Cantilever Beam, Temperature changeCalculation Example – Undamped free Vibration (Part A).Calculation Example – Undamped free Vibration (Part B).Calculation Example – Evaluation of Structural Property Matrices.Calculation Example – Angular acceleration, angular velocity.Calculation Example – Shear bolt connection EC3.Calculation Example – Buckling of Column (EC3).Calculation Example - Calculate the member diagrams.Calculation Example - Calculate the member diagrams.Calculation Example - Calculate the equation of the elastic curve.Calculation Example - Calculate the location of support.Calculation Example – Plane stress.Calculation Example - Annular cross section, Stress.Calculation Example – Allowable shear force for the girder.Calculation Example - Calculate the deflection. Castigliano Theorem.Calculation Example – Determine the shear force and moment.Calculation Example – Determine the magnitudes of F1,F2.Calculation Example – Internal forces.Calculation Example - Calculate the Axial Forces of the Truss Members.Calculation Example – Calculate the moments of inertia Ix and Iy.Calculation Example – Calculate shear stress for temperature load.Calculation Example – Calculate tension force using virtual work.Calculation Example – Torsional moment-Stress.Calculation Example – Reinforced Concrete Column at Stress.Calculation Example – Cantilever Beam with uniform loading.Calculation Example – Cantilever Beam with point loads.Calculation Example – Rod loadingCalculation Example – Maximum DeflectionCalculation Example – Member Diagram.Calculation Example – Minimum allowable Diameter.Calculation Example – Critical load.Calculation Example – Simple harmonic vibration part 2Calculation Example – FrictionCalculation Example – Section Modulus SCalculation Example – Plastic Neutral Axis.Calculation Example – Buckling of Column (EC3).Calculation Example – Shear bolt connection EC3.Calculation Example – Member Diagram. Triangular load.Calculation Example – Torsional moment-Stress.Calculation Example – Angular acceleration, angular velocity.Calculate the location of point loadShear bolt connection EC3Torsional Moment-StressCalculate the Axial Forces of the Truss MembersCalculate the Maximum Shear StressHow to calculate yield strengthCalculate angular velocity, angular accelerationTemperature ChangeAverage shear stress in pressure vesselAllowable shear force of the girderCalculation ExamplesCalculate the variation in length of the rodSpring Assemblies in Series/Parallel: Two Springs in SeriesTruss vs CableCalculate the vertical deflection of a beamFlexular Crack in Concrete BeamMaximum Factored Vertical ShearColumn in bucklingBeams: maximum momentNominal flexural strength of a reinforced concrete beamCalculation of the cross-sectional area and the position of centroidCalculation of the second moments of areaExample: longitudinal reinforcement for shear and torsion according to EC2
Want to read more like this?
Calculation Example – Simple harmonic vibration part 2
Oct, 04, 2017 | EducationA single point with mass m is vibrating harmonically. The displacement x from point of balance is go...
Calculation of the cross-sectional area and the position of centroid
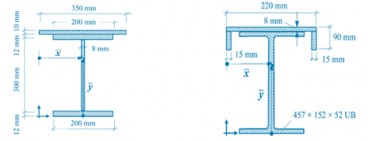
Apr, 04, 2024 | EducationThe problem: Determine the cross-sectional area and the position of the centroid for the sectio...
Calculation of the second moments of area
Apr, 12, 2024 | EducationThe problem: Determine the second moments of area, Ixx and Iyy, for the sections indicated in...
Calculation Example - Calculate the location of support.
Mar, 01, 2017 | EducationCalculate the distance x for locating roller support so that the moment on the beam at point B is ze...
Calculation Example - Calculate the equation of the elastic curve.
Jan, 25, 2017 | EducationCalculate the equation of the elastic curve .Determine the pinned beam’s maximum deflection. EI cons...
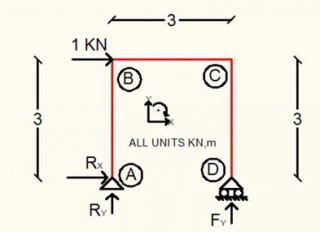
Calculation Example – Frame analysis.
Apr, 13, 2016 | EducationCalculate the reactions and member forces. Solution We calculate the reactions. Section 1 0...
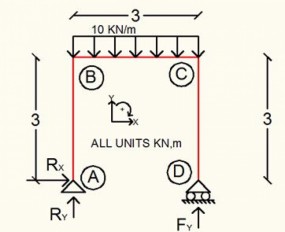
Calculation Example – Frame analysis – Uniform Load
May, 09, 2016 | EducationCalculate the reactions and member forces. Solution We calculate the reactions. ...
Calculation Example – Beam with inner hinge (Part B). Calculate the member diagrams.
Mar, 17, 2016 | EducationCalculate the member diagrams. Solution We have already calculated the external beam rea...
Beams: maximum moment
Jun, 07, 2022 | EducationFind the maximum moment of the above beam which is subjected to triangular vertical load. SOLUTION:...
Trending
Jun, 18, 2019 | Education
Calculate the Maximum Shear Stress
Sep, 16, 2022 | Education
Diaphragms
Aug, 05, 2019 | Education
How to calculate yield strength
Aug, 28, 2023 | Education
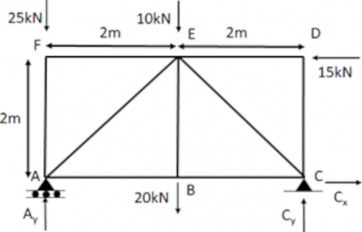
Truss deflection using the unit load method
Sep, 16, 2022 | Education
Structural stability
Jun, 29, 2023 | Education
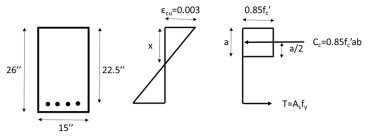
Nominal flexural strength of a reinforced concrete beam
Sep, 08, 2015 | Education
Calculation Example: Axial Force On A Column
Mar, 01, 2024 | Education
Overhanging beam: shear force and bending moment calculation
Sep, 25, 2024 | Education