Contents [show]
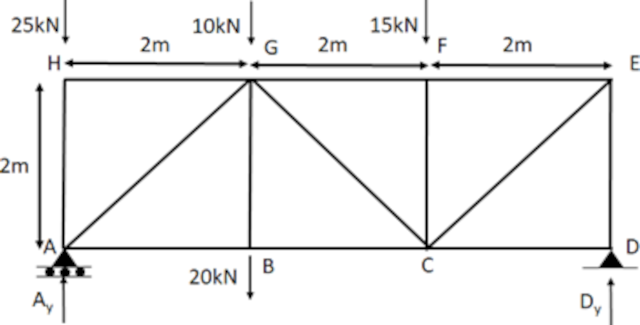
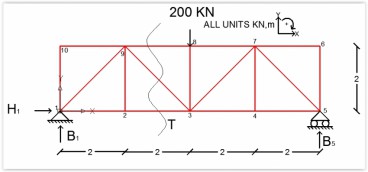
Please determine the forces in the members BC, GC and GF of the pin-jointed plane truss shown in Figure 1 using the method of sections.
Given:

Solution:
Reactions at the supports
Support A will have only vertical reaction and no horizontal reaction since it is on the roller. Support D is hinged and therefore will experience both horizontal and vertical reactions. Furthermore, the truss considered is determinate as it satisfies the condition of determinacy of plane truss: m = 2j – 3.
(i) ΣFx = 0: There is no external horizontal force acting on the truss. Therefore, the horizontal reaction at D will be zero, i.e. Dx = 0kN
(ii) ΣFy = 0 -> Ay + Dy - 25 -10 - 20 - 15 = 0 -> Ay + Dy = 70;
(iii) ΣMz = 0: Considering z-axis perpendicular to the plane and passing through joint A. Take moment of all the forces about z-axis.
ΣMz = 0 -> Ay x 0 + Dy x 6 - 20 x 2 - 15 x 4 - 10 x 2 + 25 x 0 =0 -> Dy = 120/6 -> Dy = 20kN
Therefore, from equation (i) we get Ay = 70 - 20 -> Ay =50kN
Calculation of member forces by method of sections
As it is explained in this example, method of sections is useful when we have to calculate the forces in some of the members, not all. We cut the truss into two parts through section (1) - (1) passing through GF, GC and BC. We consider the equilibrium of the left side part of the truss as shown in Figure 2. While considering equilibrium of this part we look only for the support reactions, the external forces acting on the truss, and the member forces which are cut by the section.

Let's assume the unknown forces in members GF, GC and BC as tensile as shown in Figure 2. It should be outlined that possible negative values indicate that the force is opposite to the assumed direction.
(iv) ΣFx = 0 -> FBC + FGF + FGC cos45 = 0
(v) ΣFy = 0 -> 50 - 25 - 20 -10 - FGC sin45 = 0 -> FGC sin45 = - 5 -> FGC = - 7.072kN
(vi) ΣMG = 0 -> FBC x 2 - 50 x 2 + 25 x 2 = 0 -> FBC = 25kN
Thus, substituting the value of FBC and FGC in equation (iv) we get FGF = - 20kN
Selected Topics
Want to read more like this?
Truss deflection using the unit load method
Aug, 28, 2023 | EducationGiven: A pin-jointed truss is given in Figure 1. Determine the vertical displacement of join...
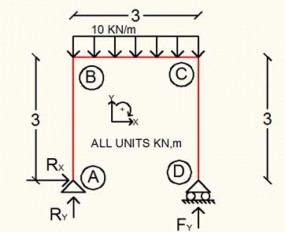
Calculation Example – Frame analysis.
Apr, 13, 2016 | EducationCalculate the reactions and member forces. Solution We calculate the reactions. Section 1 0...
Calculation Example – Frame analysis – Uniform Load
May, 09, 2016 | EducationCalculate the reactions and member forces. Solution We calculate the reactions. ...
Calculate the Axial Forces of the Truss Members
May, 16, 2019 | EducationFind the axial forces of the members 2-3, 9-3 of the truss for the given loads. Solution...

Calculate the location of point load
Feb, 14, 2019 | EducationCalculate the distance x for locating point load so that the moment on the beam at point B is zero....
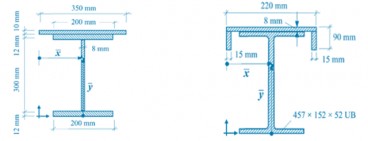
Calculation of the second moments of area
Apr, 12, 2024 | EducationThe problem: Determine the second moments of area, Ixx and Iyy, for the sections indicated in...
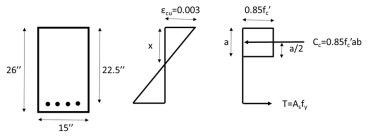
Nominal flexural strength of a reinforced concrete beam
Jun, 29, 2023 | EducationCompute the nominal flexural strength Mn of the reinforced concrete rectangular section of Figure...

Beams: maximum moment
Jun, 07, 2022 | EducationFind the maximum moment of the above beam which is subjected to triangular vertical load. SOLUTION:...

Calculation of the cross-sectional area and the position of centroid
Apr, 04, 2024 | EducationThe problem: Determine the cross-sectional area and the position of the centroid for the sectio...
Trending

Diaphragms

Calculate the Maximum Shear Stress
Structural stability

Overhanging beam: shear force and bending moment calculation

Calculation Example – Plastic Neutral Axis.

An engineering point of view for the Tacoma Narrows Bridge collapse

Calculation Example – Beam with inner hinge (Part A). Find the Reactions