Calculation Example: Calculate the Change in Length of a Rod loaded in extension

Contents [show]
The rod of the picture is loaded with the force P2 which is uniformly distributed on Section D where applied.
If the material of the rod is homogeneous and elastic with Elastic Modulus E find the variation in length of the rod. The area of the cross section in part AC is F1 while CD is F2.

Solution
We calculate the reaction RA at the rigid end connection A from the equilibrium of forces.
The rod doesn’t have constant area of cross sectional area so we examine parts AC and CD.
For AC the cross sectional area F1 is loaded with axial force equal to RA. So the uniform stress ?1 and deformation ?1 are:
Since the material is homogeneous and elastic Hooke's Law is applied for section AC.
(2)
For section CD the axial force P2 is:
And Hooke's Law:
(3)
From equations (1),(2),(3) we have the total variation of length of the rod is:
Where
Selected Topics
Want to read more like this?

Calculate the variation in length of the rod
Apr, 06, 2020 | EducationThe rod of the picture is loaded with the force 2P which is uniformly distributed on Section D wher...

Calculation Example – Rod loading
Oct, 04, 2017 | EducationCalculate the internal normal forces at points A,B,C for the rod which is loaded with the forces sho...

Calculation Example - Annular cross section, Stress.
Mar, 01, 2017 | EducationA strain gage is located at D on the surface of the rod AB. The average normal stress on the rod is...

Calculation Example - Calculate the Axial Forces of the Truss Members.
Aug, 21, 2017 | EducationFind the axial forces of the members 2-3, 9-3 of the truss for the given loads. Soluti...

Calculation Example - Calculate the Axial Forces on the Truss Members
Jan, 20, 2016 | EducationFind the axial forces of the members 2-3, 3-9 of the truss for the given external loads. ...

Calculation Example - Calculate the member diagrams.
Jan, 25, 2017 | EducationCalculate the member diagrams for the point load P for the pinned beam at two ends. Solut...
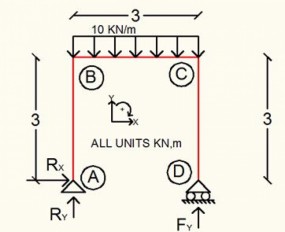
Calculation Example – Frame analysis – Uniform Load
May, 09, 2016 | EducationCalculate the reactions and member forces. Solution We calculate the reactions. ...
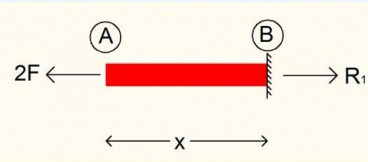
Calculation Example – Cantilever Beam, Temperature change
Aug, 17, 2016 | EducationThe beam is fixed at end B and free at end A. It is loaded at end A with the concentrated force 2F....

Calculation Example - Calculate the member diagrams.
Aug, 17, 2016 | EducationCalculate the member diagrams for the uniform loading q for the pinned beam at two ends. So...
Trending

Diaphragms
Structural stability
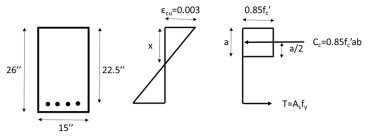
Nominal flexural strength of a reinforced concrete beam

Calculate the Maximum Shear Stress
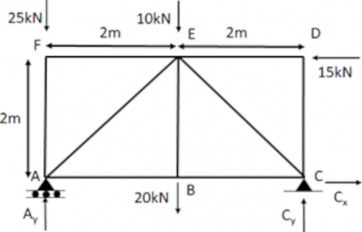
Truss deflection using the unit load method

Overhanging beam: shear force and bending moment calculation

Calculation Example – Beam with inner hinge (Part A). Find the Reactions

