Bending stress in a beam element
Contents [show]
Given:
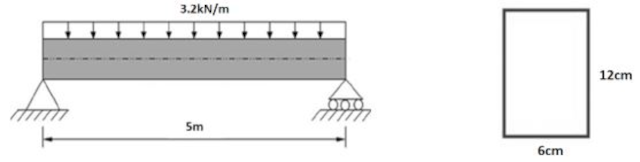
A simply supported beam of length L=5m is given in Figure 1a. The beam is subjected to uniform distributed load equal to 3.2kN/m. If the beam has a rectangular cross-section, as shown in Figure 1b, calculate the absolute maximum bending stress in the beam and draw the bending stress diagram.

Solution:
The bending stress of a beam element is calculated using the bending equation, i.e. M / I = σ / y, where M is the bending moment, I is the moment of inertia about the neutral axis (N.A.) of the section, σ is the bending stress and y is the distance from the neutral axis to the point of bending stress. In other words, we can write that:
σ = M y / I (1)
The above relation shows that the bending stress will be maximized if the distance y becomes maximum, i.e. at the top or bottom of the section. The latter is translated to a distance of 5cm from the neutral axis of the section. It is pointed out that the absolute maximum bending stress concerns the section of the maximum bending moment.
Moreover, the given beam is simply supported with uniform loading on the entire span. Thus, the maximum bending moment will occur at the mid-span of the beam and is calculated following the formula Mmax = q L2/8, where q is the uniform load on the beam and L is the span of the beam. The maximum bending moment is:
Mmax = 3.2 x 52 / 8 = 10kNm (2)
For a rectangular section, the moment of inertia Ixx, about the neutral axis, is calculated as:
Ixx = bd3/12 = 6 x 123 / 12 = 0.864 x 103cm4 = 0.864 x 10-5 m4 (3)
Using Eq. 1, the absolute maximum bending stress is calculated as:
σmax = (Mmax) (ymax) / (Ixx) = 10kNm x 0.06m / (0.864 x 10-5m4) = 0.694 x 105 kN/m2 = 69.4 MPa
The bending stress diagram is shown in Figure 2. The bending stress above the neutral axis (N.A.) is compressive (negative) while the bending stress below the neutral axis is tensile (positive).

Selected Topics
Want to read more like this?

Overhanging beam: shear force and bending moment calculation
Mar, 01, 2024 | EducationCalculate the shear force and bending moment values due to the imposed loading on the overhanging...

Calculate the Maximum Shear Stress
Jun, 18, 2019 | EducationA steel bar with diameter d = 14 mm is subjected to a tensile load P = 10 kN (see figure). (a) What...

Calculation Example - Calculate the member diagrams
Feb, 04, 2016 | EducationCalculate the member diagrams for Axial Force N, Shear Force S and bending Moment M for the followin...

Calculation Example - Calculate the member diagrams for the beam
Feb, 16, 2016 | EducationCalculate the member diagrams for Axial Force N, Shear Force Q and bending Moment M for the followin...
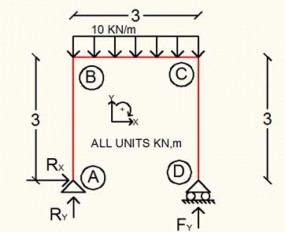
Calculation Example – Frame analysis – Uniform Load
May, 09, 2016 | EducationCalculate the reactions and member forces. Solution We calculate the reactions. ...
Torsional Moment-Stress
Apr, 17, 2019 | EducationCalculate the max stress because of torsional moment on the outer layer of a steel hollow rod when t...

Cross Section Analysis and Design
Nov, 01, 2013 | Software
Optimal Beam (Structural Beam Calculator)
Jan, 14, 2019 | SoftwareBeams
Sep, 14, 2023 | EducationBeam, in structural engineering, is a horizontal structural element that is designed to carry and...
Trending

Diaphragms
Structural stability
Nominal flexural strength of a reinforced concrete beam
Truss deflection using the unit load method

Calculation Example – Beam with inner hinge (Part A). Find the Reactions

Method of sections

Calculation Example – Plastic Neutral Axis.