Calculate the variation in length of the rod

Contents [show]
The rod of the picture is loaded with the force 2P which is uniformly distributed on Section D where applied. If the material of the rod is homogenous with Elastic Modulus E find the variation in length of the rod. The area of the cross section in part AC is 2A while CD is A.
Solution
We calculate the reaction R at the rigid end connection A from the equilibrium of forces.
ΣPX= 0 → 2P - R = 0 → R = 2P (1)
The rod doesn’t have everywhere constant area of cross section so we examine parts AC and CD.
At part AC the cross section with area 2A is loaded with axial force equal to R. So at this part we have equal uniform stress σ1 and deformation ε1.
σ1 = R / 2A
ε1 = Δl1 / L
Because stress is equal and the material is homogenous Hook Law is applied for section AC.
σ1= Eε1 → R / 2A = E ( Δl1 / L) →Δl1 = (R / 2A) (L / E) (2)
At part CD we have axial force 2P so:
σ2 = 2P / A
ε2 = Δl2 / 3L
And Hooks Law:
σ2 = Eε2 → 2P / A = E (Δl2 / 3L) → Δl2= (2P / A )(3L / E) (3)
From equations (1),(2),(3) we have the total change of length of the rod.
Δl= Δl1 + Δl2 = (R / 2A)(L / E) + (2P / A)(3L / E)
Selected Topics
Want to read more like this?

Calculation Example: Calculate the Change in Length of a Rod loaded in extension
Jan, 12, 2016 | EducationThe rod of the picture is loaded with the force P2 which is uniformly distributed on Section D where...

Shear bolt connection EC3
Mar, 18, 2019 | EducationCheck the shear connection for the IPE450-S275 for the design shear VEd=500KN. Bolts M20-8.8, plate...

Calculate the location of point load
Feb, 14, 2019 | EducationCalculate the distance x for locating point load so that the moment on the beam at point B is zero....

Calculation Example: Natural Periods of Vibration for Systems
Jul, 30, 2015 | EducationEach of the following columns supports a block of identical mass, m. The columns are fixed at the bo...
Torsional Moment-Stress
Apr, 17, 2019 | EducationCalculate the max stress because of torsional moment on the outer layer of a steel hollow rod when t...

Calculation Example – Shear bolt connection EC3.
Oct, 04, 2017 | EducationCheck the shear connection for the IPE450-S275 for the design shear VEd=300KN. Bolts M20-8.8, plate...

Beams: maximum moment
Jun, 07, 2022 | EducationFind the maximum moment of the above beam which is subjected to triangular vertical load. SOLUTION:...
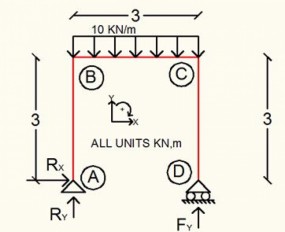
Calculation Example – Frame analysis – Uniform Load
May, 09, 2016 | EducationCalculate the reactions and member forces. Solution We calculate the reactions. ...
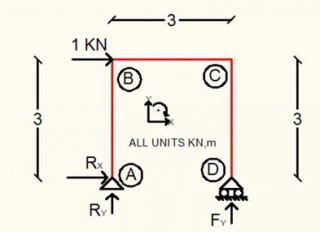
Calculation Example – Frame analysis.
Apr, 13, 2016 | EducationCalculate the reactions and member forces. Solution We calculate the reactions. Section 1 0...
Trending

Diaphragms
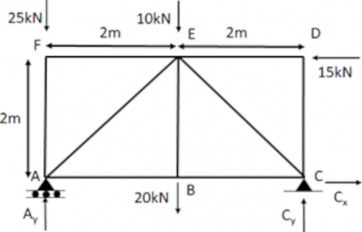
Truss deflection using the unit load method
Structural stability
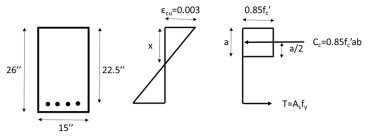
Nominal flexural strength of a reinforced concrete beam

Overhanging beam: shear force and bending moment calculation

Calculate the Maximum Shear Stress

Calculation Example – Plastic Neutral Axis.